数据结构课设：多叉路口交通灯管理问题

题目描述

通常，在十字交叉路口只需设红、绿两色的交通灯便可保持正常的交通秩序，而在多叉路口需设几种颜色的交通灯才能既使车辆相互之间不碰撞，又能达到车辆的最大流通。假设有一个如图(a)所示的五叉路口，其中C和E为单行道。在路口有13条可行的通路，其中有的可以同时通行，如A→B和E→C，而有的不能同时通行，如E→B和A→D。那么，在路口应如何设置交通灯进行车辆的管理呢？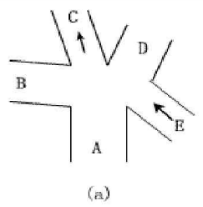

思路分析

顶点图解释：

1. 圈XY代表从道路X驶向道路Y的通道。
2. 共有2×C（3，2）+4+3共13条通道。
3. 若两通道不能同时通行，则将两通道相连。
   

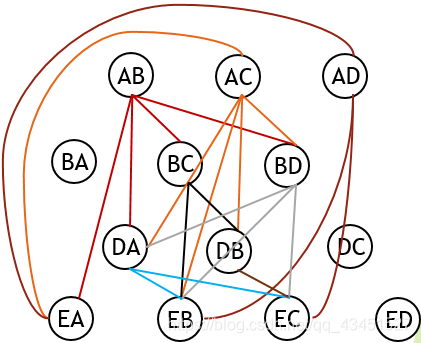
问题转化为图着色问题

用最少的颜色对图着色<=>对尽可能多的点着以相同的颜色<=>让尽可能多的通道的车辆可以同时通行=>车流量最大

邻接矩阵

按图里从左到右从上到下的顺序对13个顶点从0~12依次标号，然后按照两顶点之间有边相连值为1，无边相连值为0的规则，得到邻接矩阵，如下：
0 0 0 0 1 1 1 0 0 1 0 0 0
0 0 0 0 0 1 1 1 0 1 1 0 0
0 0 0 0 0 0 0 0 0 1 1 1 0
0 0 0 0 0 0 0 0 0 0 0 0 0
1 0 0 0 0 0 0 1 0 0 1 0 0
1 1 0 0 0 0 1 0 0 0 1 1 0
1 1 0 0 0 1 0 0 0 0 1 1 0
0 1 0 0 1 0 0 0 0 0 0 1 0
0 0 0 0 0 0 0 0 0 0 0 0 0
1 1 1 0 0 0 0 0 0 0 0 0 0
0 1 1 0 1 1 1 0 0 0 0 0 0
0 0 1 0 0 1 1 1 0 0 0 0 0
0 0 0 0 0 0 0 0 0 0 0 0 0

算法

算法1：回溯法（深度优先搜索）

思路：

1. 假设符合题意的最小颜色数是m
2. 则每一个顶点可以涂m种颜色，共m^13种可能（包括合理和不合理的涂色方案）
3. 采用深度优先搜索算法，找到合理的涂色方案，如果找不到则增加最小颜色数继续查找

该算法一定得到最优解，但时间复杂度高。

算法2：贪婪算法（Welch Powell算法）

1. 将顶点按度数由大到小排列
2. 对未涂色的度数最大的顶点涂色，并将与该顶点不相连且满足条件的其它顶点涂以相同的颜色
3. 检查是否存在未涂色的顶点，若有，换一种颜色，重复2），否则，结束算法

该算法是启发式算法，时间复杂度低，但不一定得到最优解。

算法源码

算法1

#include <iostream>
using namespace std;

//颜色类 
class Color {
    public:
        Color(int n,int **a,int *x,int sum);
        bool ifOk(int node);
        void Dfs(int node);
        int n;        //顶点数
        int m;        //可用颜色数
        int **a;    //邻接矩阵
        int *x;        //解向量
        int sum;    //可着色方案数
};

//构造函数 
Color::Color(int n,int **a,int *x,int sum){
    this->n=n;
    this->a=a;
    this->x=x;
    this->sum=sum;        
}

//判断顶点node是否可以涂色 
bool Color::ifOk(int node) {
    for (int i = 1; i <= n; i++) 
        if ((a[node-1][i-1] == 1) && x[node] == x[i])
            return false;
    return true;
}

//深度优先搜索 
void Color::Dfs(int node) {
    //当访问到叶子结点，则找到一种可着色方案 sum++
    if (node > n) {
        sum++;
        //输出该涂色方案 
        for (int i = 1; i <= n; i++)
            cout << x[i] << " ";
        cout << endl;
    }
    //递归 
    else {
        for (int i = 1; i <= m; i++) {
            x[node] = i;
            if (ifOk(node))
                Dfs(node + 1);
            x[node] = 0;
        }
    }
}

int main() {
    //初始化邻接矩阵 
    int** graph=new int*[13];
    for(int i=0;i<13;i++)
        graph[i]=new int[13];
    for (int i = 0;i < 13;i++)
        for (int j = 0;j < 13;j++)
            cin >> graph[i][j];

    //初始化解向量 
    int* p=new int[14];
    for(int i=0;i<14;i++)
        p[i]=0;

    //初始化颜色类 
    Color color(13,graph,p,0);

    //涂色 
    int k=0;
    while(true){
        k++;
        color.m=k;
        color.Dfs(1);
        if(color.sum!=0)
            break;
    }

    //输出最小颜色数和涂色方案数 
    cout<<"最小颜色数m为："<<k<<endl; 
    cout<<"可行的涂色方案数为："<<color.sum;
}

算法2

#include <iostream>
#include <queue> 
using namespace std;
struct Node {
    int index;
    int degree;
    int color;
};

//冒泡排序 
void sort(Node* nodes) {
    for (int i = 0;i < 13;i++) {
        for (int j = 12;j > i;j--) {
            if (nodes[j].degree > nodes[j - 1].degree) {
                int degree = nodes[j - 1].degree;
                int index = nodes[j - 1].index;
                nodes[j - 1].degree = nodes[j].degree;
                nodes[j - 1].index = nodes[j].index;
                nodes[j].degree = degree;
                nodes[j].index = index;
            }

        }
    }
}

//按度数递减顺序输出排序后的顶点 
void output(Node* nodes){
    queue<int> q0,q1,q2,q3,q4,q5;
    queue<int> q[6]; 
    for(int i=0;i<13;i++)
        q[nodes[i].degree].push(nodes[i].index);
    for(int i=5;i>=0;i--){
        cout<<"度数为"<<i<<"的顶点：";
        if(q[i].empty())
            cout<<"无";
        while(!q[i].empty()){
            int index=q[i].front( );
            cout<<index<<" ";
            q[i].pop();
            } 
            cout<<endl;
        }
}

//判断顶点nodes[j]是否可以涂上颜色color 
bool ifOk(Node* nodes,int** graph,int color,int j){
    if(nodes[j].color!=0)
        return false;
    for(int i=0;i<13;i++)
            if(graph[nodes[j].index][i]==1)
                for(int m=0;m<13;m++)
                    if(nodes[m].index==i)
                        if(nodes[m].color==color)
                            return false;
    return true;
} 

int main() {
    //初始化邻接矩阵 
    int** graph=new int*[13];
    for(int i=0;i<13;i++)
        graph[i]=new int[13];
    //初始化顶点数组，记录13个顶点的索引、度数、颜色    
    Node* nodes = new Node[13];
    for (int i = 0;i < 13;i++) {
        int degree = 0;
        for (int j = 0;j < 13;j++) {
            cin >> graph[i][j];
            if (graph[i][j])
                degree++;
        }
        nodes[i].index = i;
        nodes[i].degree = degree;
        nodes[i].color = 0;
    }

    //对顶点按度数递减排序 
    sort(nodes);
    //输出排序后的结果 
    cout<<"按度数由大到小排序后的结果："; 
    for(int i=0;i<13;i++){
        cout<<nodes[i].index<<" ";
        if(i==12)
            cout<<endl;
    }
    output(nodes);

    //对13个顶点采用贪婪算法进行迭代涂色 
    int k = 0;
    while (true) {
        k++;
        int i;
        for (i = 0;i < 13;i++) 
            if (nodes[i].color == 0) {
                nodes[i].color = k;
                break;
            }

        if (i == 13)
            break;

        for (int j = 0;j < 13;j++)
            if (ifOk(nodes,graph,k,j))
                nodes[j].color = k;
    }

    //输出所需最小颜色数和一种涂色方案 
    cout <<"所需要的最小颜色数目："<<k-1<<endl;
    cout<<"一种涂色方案为："<<endl;
    for(int i=1;i<k;i++){
        cout<<i<<':';
        for(int j=0;j<13;j++)
            if(nodes[j].color==i)
                cout<<nodes[j].index<<' ';
        if(i<k-1)
            cout<<endl;
    }
}

谢谢阅读，如果有用可否点个赞O(∩_∩)O